In the system of rotation of two cosmic bodies of a certain mass, there are points in space, by placing any object of small mass in which, you can fix it in a stationary position relative to these two bodies of rotation. These points are called Lagrange points. The article will discuss how they are used by humans.
What are Lagrange points?
To understand this issue, one should turn to solving the problem of three rotating bodies, two of which have such a mass that the mass of the third body is negligible compared to them. In this case, it is possible to find positions in space in which the gravitational fields of both massive bodies will compensate for the centripetal force of the entire rotating system. These positions will be the Lagrange points. By placing a body of small mass in them, one can observe how its distances to each of the two massive bodies do not change for an arbitrarily long time. Here we can draw an analogy with the geostationary orbit, where the satellite is alwayslocated above one point on the earth's surface.
It is necessary to clarify that the body that is located at the Lagrange point (it is also called a free point or point L), relative to an external observer, moves around each of the two bodies with a large mass, but this movement in conjunction with the movement of the two remaining bodies of the system has such a character that with respect to each of them the third body is at rest.
How many of these points and where are they located?
For a system of rotating two bodies with absolutely any mass, there are only five points L, which are usually denoted L1, L2, L3, L4 and L5. All these points are located in the plane of rotation of the considered bodies. The first three points are on the line connecting the centers of mass of two bodies in such a way that L1 is located between the bodies, and L2 and L3 behind each of the bodies. Points L4 and L5 are located so that if you connect each of them with the centers of mass of two bodies of the system, you will get two identical triangles in space. The figure below shows all the Earth-Sun Lagrange points.
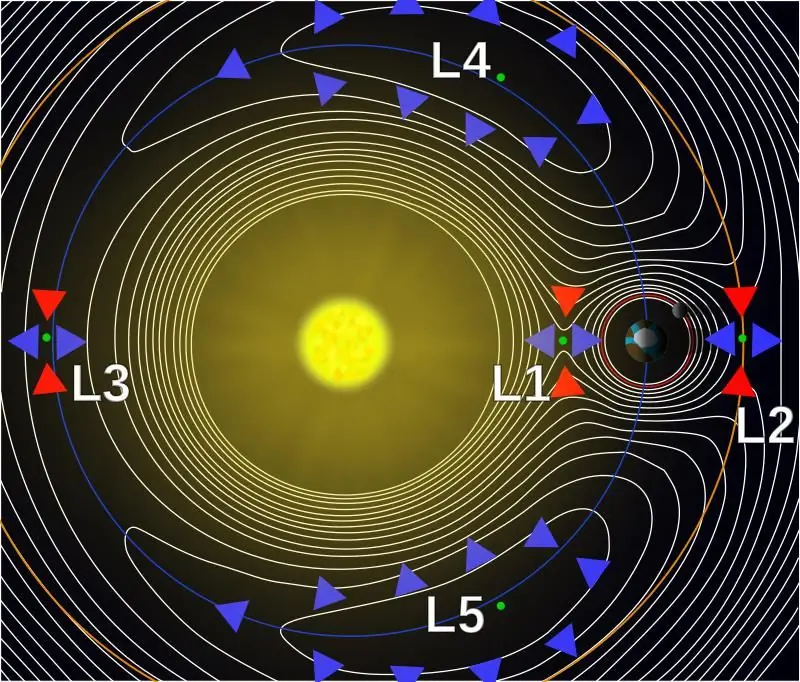
The blue and red arrows in the figure show the direction of the resultant force when approaching the corresponding free point. It can be seen from the figure that the areas of points L4 and L5 are much larger than the areas of points L1, L2 and L3.
Historical background
For the first time, the existence of free points in a system of three rotating bodies was proved by the Italian-French mathematician Joseph Louis Lagrange in 1772. To do this, the scientist had to introduce some hypotheses anddevelop your own mechanics, different from Newtonian mechanics.
Lagrange calculated the points L, which were named after his name, for ideal circular orbits of revolution. In reality, the orbits are elliptical. The latter fact leads to the fact that there are no longer Lagrange points, but there are areas in which the third body of small mass makes a circular motion similar to the movement of each of the two massive bodies.
Free point L1

The existence of the Lagrange point L1 is easy to prove using the following reasoning: let's take the Sun and the Earth as an example, according to Kepler's third law, the closer the body is to its star, the shorter its period of rotation around this star (the square of the period of rotation of the body is right proportional to the cube of the average distance from the body to the star). This means that any body that is located between the Earth and the Sun will revolve around the star faster than our planet.
However, Kepler's law does not take into account the influence of gravity of the second body, that is, the Earth. If we take this fact into account, then we can assume that the closer the third body of small mass is to the Earth, the stronger will be the opposition to the Earth's solar gravity. As a result, there will be such a point where the Earth's gravity will slow down the speed of rotation of the third body around the Sun in such a way that the periods of rotation of the planet and the body will become equal. This will be the free point L1. The distance to the Lagrange point L1 from the Earth is 1/100 of the radius of the planet's orbit aroundstars and is 1.5 million km.
How is the L1 area used? It is an ideal place to observe the solar radiation as there are never any solar eclipses here. Currently, several satellites are located in the L1 region, which are engaged in the study of the solar wind. One of them is the European artificial satellite SOHO.
As for this Earth-Moon Lagrange point, it is located approximately 60,000 km from the Moon, and is used as a "transit" point during missions of spacecraft and satellites to and from the Moon.
Free point L2

Arguing similarly to the previous case, we can conclude that in a system of two bodies of revolution outside the orbit of a body with a smaller mass, there should be an area where the drop in centrifugal force is compensated by the gravity of this body, which leads to the alignment of the periods of rotation of a body with a smaller mass and a third body around a body with a larger mass. This area is a free point L2.
If we consider the Sun-Earth system, then to this Lagrange point the distance from the planet will be exactly the same as to point L1, that is, 1.5 million km, only L2 is located behind the Earth and farther from the Sun. Since there is no influence of solar radiation in the L2 region due to the earth's protection, it is used to observe the Universe, having various satellites and telescopes here.
In the Earth-Moon system, point L2 is located behind the Earth's natural satellite at a distance of 60,000 km from it. In lunar L2there are satellites that are used to observe the far side of the moon.
Free points L3, L4 and L5
Point L3 in the Sun-Earth system is behind the star, so it cannot be observed from the Earth. The point is not used in any way, as it is unstable due to the influence of the gravity of other planets, such as Venus.
Points L4 and L5 are the most stable Lagrange regions, so there are asteroids or cosmic dust near almost every planet. For example, only cosmic dust exists at these Lagrange points of the Moon, while Trojan asteroids are located at L4 and L5 of Jupiter.

Other uses for free dots
In addition to installing satellites and observing space, the Lagrange points of the Earth and other planets can also be used for space travel. It follows from the theory that moving through the Lagrange points of different planets is energetically favorable and requires little energy.
Another interesting example of using the Earth's L1 point was the physics project of a Ukrainian schoolchild. He proposed to place a cloud of asteroid dust in this area, which would protect the Earth from the destructive solar wind. Thus, the point can be used to influence the climate of the entire blue planet.






